- 4
- 국내산라이츄
- 조회 수 1022

하루에 두편이나 쓰다니...
1. 그래프?
여기서 말하는 그래프는 꼭지점과 변으로 객체간의 연결 관계를 표현한 것으로, 그 자체로 어떤 '정보'를 전달하는 수단이 되기도 합니다. 예? 주식 그래프 보면 한강물 온도 체크하는 그런거요? 꺾은선! 막대! 아니 그거 아니라니까 이사람들아. 여기서 말하는 그래프는 '일부 객체들의 쌍이 서로 연관된 객체의 집합을 이루는 구조'로 정의하는 거예요. 꼭지점(V)과 변(E)의 순서쌍 집합을 통해 G=(V,E)로 정의하고... 저거 튜플임다.
딥러닝 관련 논문을 보면 각 층으로 어떻게 정보가 전달되는지를 알려주는데, 그 때 노드간의 연결을 화살표로 표기합니다. 그래서 모식도는 유향 그래프예요. 변이 화살표그덩. 아니 좀 확 와닿는 예제 없어요? 아 기다려봐요.
이것도 7호선이 부평구청까지인 걸 보니 좀 올드한 노선도긴 한데 아무튼... 더 올드한거는 어떻게 되냐고요? 저 초딩때 7호선 종점 온수도 아니고 건대입구였습니다. 호랑이 담배피던 시절인데 원흥역도 없었고 6호선도 없었음... 중앙선이요? 아니 없었는데요? 중앙선 상봉역이 나 고등학교 졸업하고 생겼지 아마... 경의선도 쟈철 아니었습니다. 지금은 쟈철이지만. 그리고 하남시 지하철로 못갔었음... (지금은 5호선 연결됐죠)
아니 그래프 얘기하다말고 뭔 지하철 썰이여... 아니 저것도 일종의 그래프입니다. 일단 더럽게 복잡하고 6호선에 버뮤다 응암지대가 있긴 하지만... 아니 근데 저거 저러다가 화성까지... 어? 서동탄 연결됐네? 이사람 참고로 아직도 동탄이 어디인지 모름
아까 그래프는 꼭지점과 변으로 연결되어 있고 어떠한 정보를 전달하는 수단이 된다고 했는데... 그거랑 연관지어보면 왜 저게 그래프의 예시인 지 알 수 있습니다. 봐봐 다 동그라미제. 선으로 연결되어 있죠. 역간의 연결 정보를 제공하고 있습니다. 실제 지형은 반영 안 됐지만... 자자 잘 봐봐요. 내가 오랜만에 스울 올라온 친구랑 강남역에서 밥을 묵기로 했어요. 근데 내가 지금 밖인디 성수역 근처여. 글믄 지하철을 타고 가야쓰것쥬? 이 때 지하철 노선도를 통해 두 가지 정보를 얻을 수 있습니다. 첫째는 어떤 순환선을 타고 가야 빨리 도착하는가(2호선은 외선/내선순환으로 나뉩니다. 신설동/까치산행은 그거 타는 역에서 선로가 나뉨), 빨리 도착하는 순환선을 타면 몇 정거장인가.
저거 응암순환에 화살표 있는 거 보면 일단 그 부분은 유향같은데, 기본적으로 지하철 노선도는 역에 붙어있는 행선지별 노선도를 제외하면 무향입니다. 그니까 쟤는 무향임. 행선지별 노선도는 꼭지점마다 화살표만 안 그렸지 사실상 종점을 가리키고 있으니까 유향같은디...?
이것도 일종의 그래프입니다. (버스 노선도) 정류장이 꼭지점, 연결관계가 변이고 지하철 노선도와 마찬가지로 여기서 여기까지 몇 정거장인가에 대한 정보를 제공합니다. 단, 버스 정류장은 이름이 같더라도 아이디가 다르니 네이버 지도에서 한번 확인해보시고 타는 편이 좋습니다. 아니 저는 우리집 정류장 아이디는 다 외웠...다기보단 31년째 사는데 버스정류장 위치도 모르는 게 이상한 거 아닙니까...
2. 그래프 이론 용어
참고로... 이거 개많습니다... 용어가 많아요... 일단 최대한 쉽고 간결하게 풀어는 드리겠으나... 복잡합니다. 그리고 복잡하다면 정상입니다.
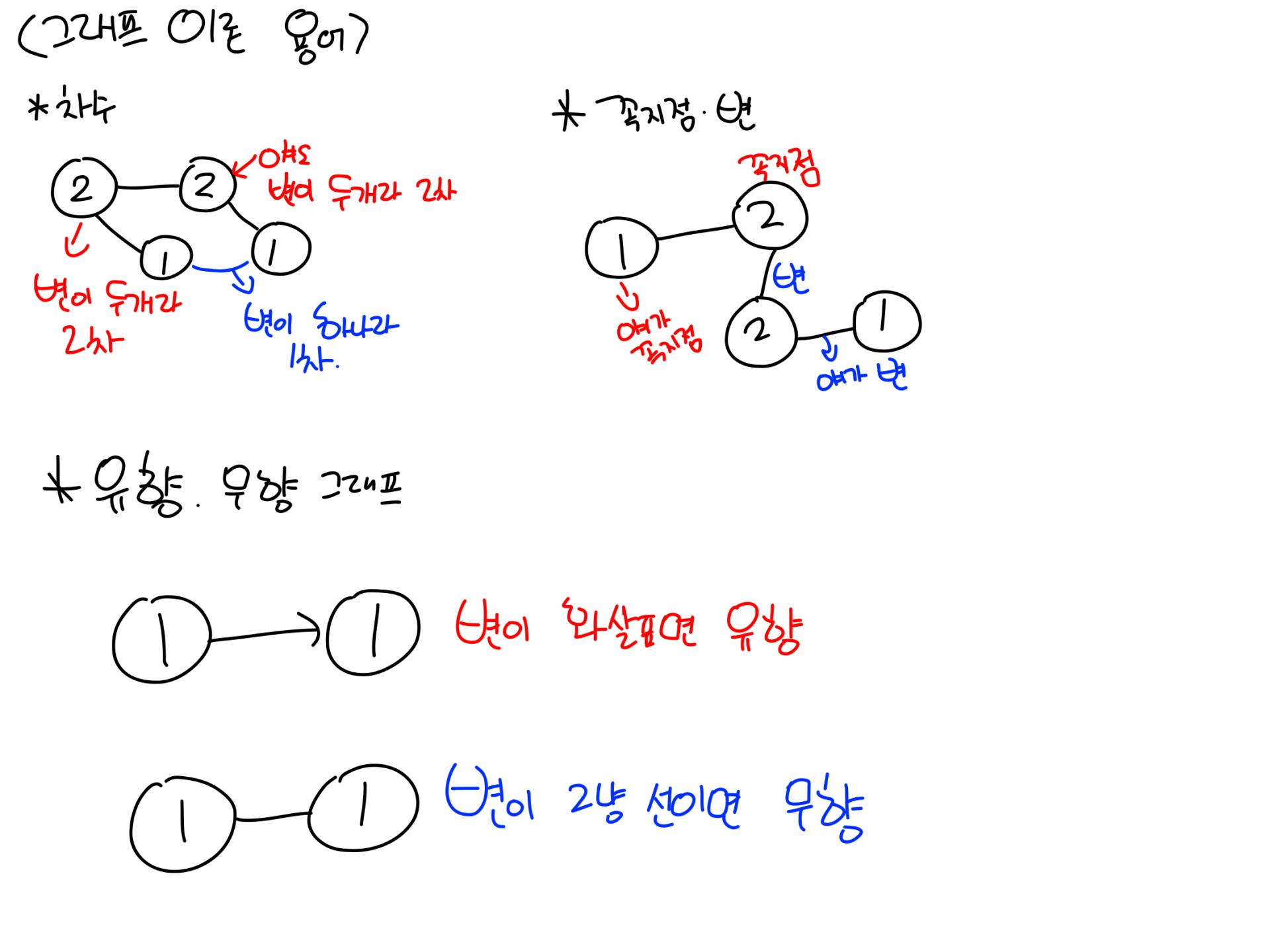
*차수: d(v)로 표기하며, 그래프에서 꼭지점에 연결된 변의 수를 말합니다. 무향 그래프는 걍 차수지만 유향 그래프는 화살표 방향에 따라 입차수(화살표 머리가 꼭지점을 향하는 것)와 출차수(화살표가 해당 꼭지점에서 나가는 것)로 나뉘어 있습니다.
*유향/무향 그래프: 변이 화살표이면 유향, 그냥 직선이면 무향 그래프입니다.
*꼭지점: 노드(저기 동그라미)
*변: 노드를 연결하는 선(저기 선)
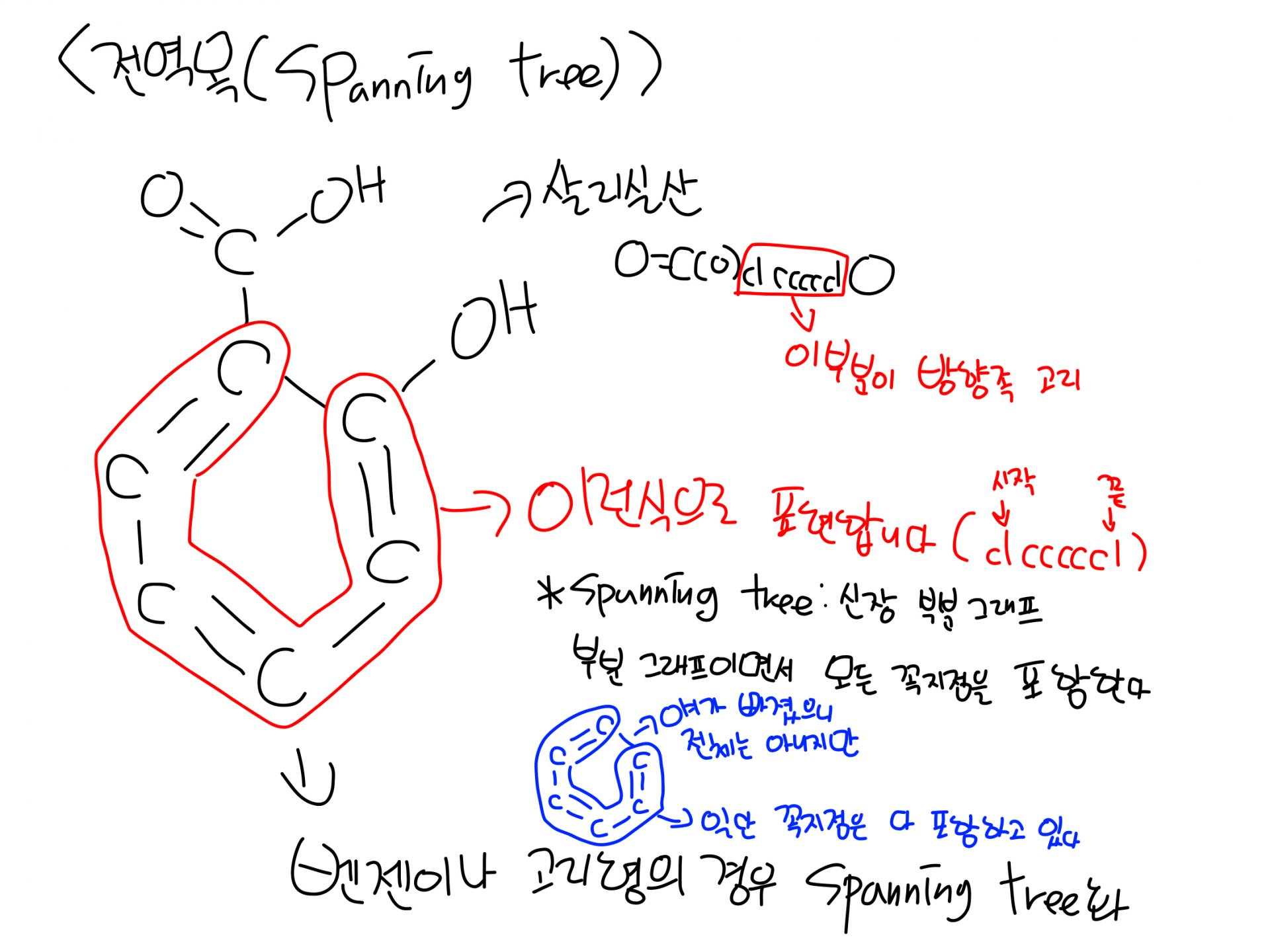
*전역목(부분 신장 그래프, spanning tree): 어떤 그래프의 부분 그래프(어떤 그래프의 꼭지점이나 변의 일부만 포함하는 그래프)이면서 모든 꼭지점을 포함하는 그래프(위 그림을 보시면 변 하나는 빠졌습니다)
*하중 그래프: 보통 딥러닝 모식도에서 많이 보는 그래프인데 말 그대로 하중이 달려있는 그래프를 말합니다. 위의 노선도를 예시로 들자면 성수에서 강남까지 가는데 각 정류장별로 몇 분이나 걸리는가 써있으면 하중 그래프입니다. 그럴거면 친구를 성수역으로 불러요
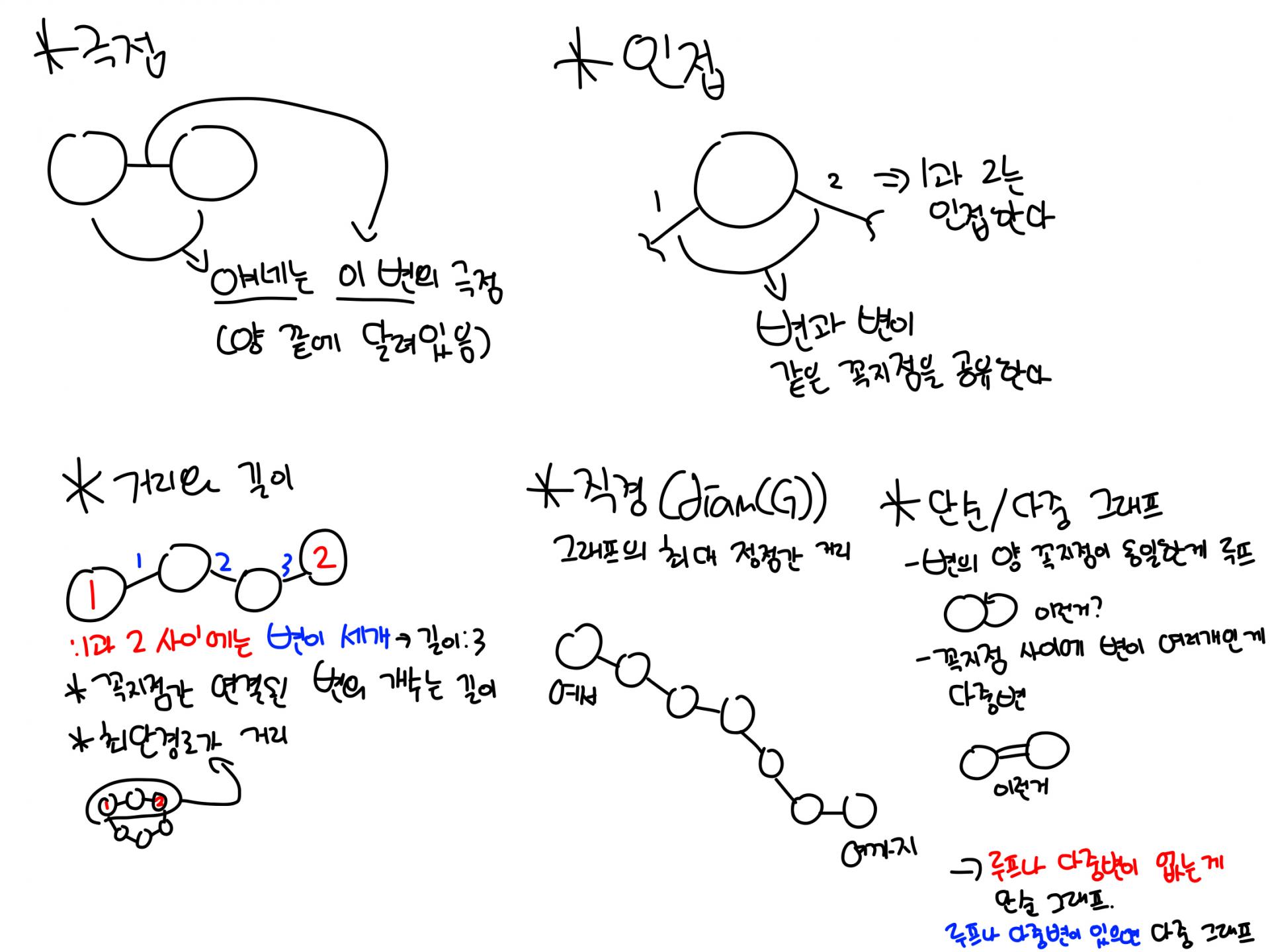
*극점: 어떤 변의 양 끝점
*인접: 두 변이 같은 꼭지점에 연결되어 있을 때, '인접한다'고 합니다. 어린이대공원역과 중곡역은 둘 다 군자역에 연결되어 있으므로 인접한 관계라고 할 수 있습니다.
*길이: 어떤 꼭지점에서 다른 꼭지점까지 연결한 변의 개수(어린이대공원역에서 장암까지 몇 정거장임?)
*거리: 어떤 꼭지점에서 다른 꼭지점까지 가는 최단거리(어린이대공원역에서 녹번역까지 가는 최단경로) 녹번역에 뭐 있는데요 형부네 식당이요 사장님 소문듣고와쓰요 유린기 하나 주이소 가능? 엄마한테 드롭킥 맞지 않을까
*직경: diam(G)로 표기. 그래프의 최대 정점간 거리를 뜻합니다. 3호선 대화역에서 오금역까지 거리. 6호선은 뭘로 재나요 저기 응암지대 끝에 저거? 참고로 7호선은 장암-건대였다가 장암-온수였다가 장암-부평구청이었다가 장암-석남됐습니다... 여기서 또 연장하면 거리 늘어나요...
*루프: 변의 양 꼭지점이 동일한 것(그니까 자기 자신이랑 연결된 거) 재귀함수같은 건가요 그게 뭔데요
*다중변: 꼭지점 사이에 변이 두 개 이상인 것
*단순/다중 그래프: 루프나 다중변이 없는 그래프를 단순 그래프라고 하고, 루프나 다중변이 있는 그래프를 다중 그래프라고 합니다.
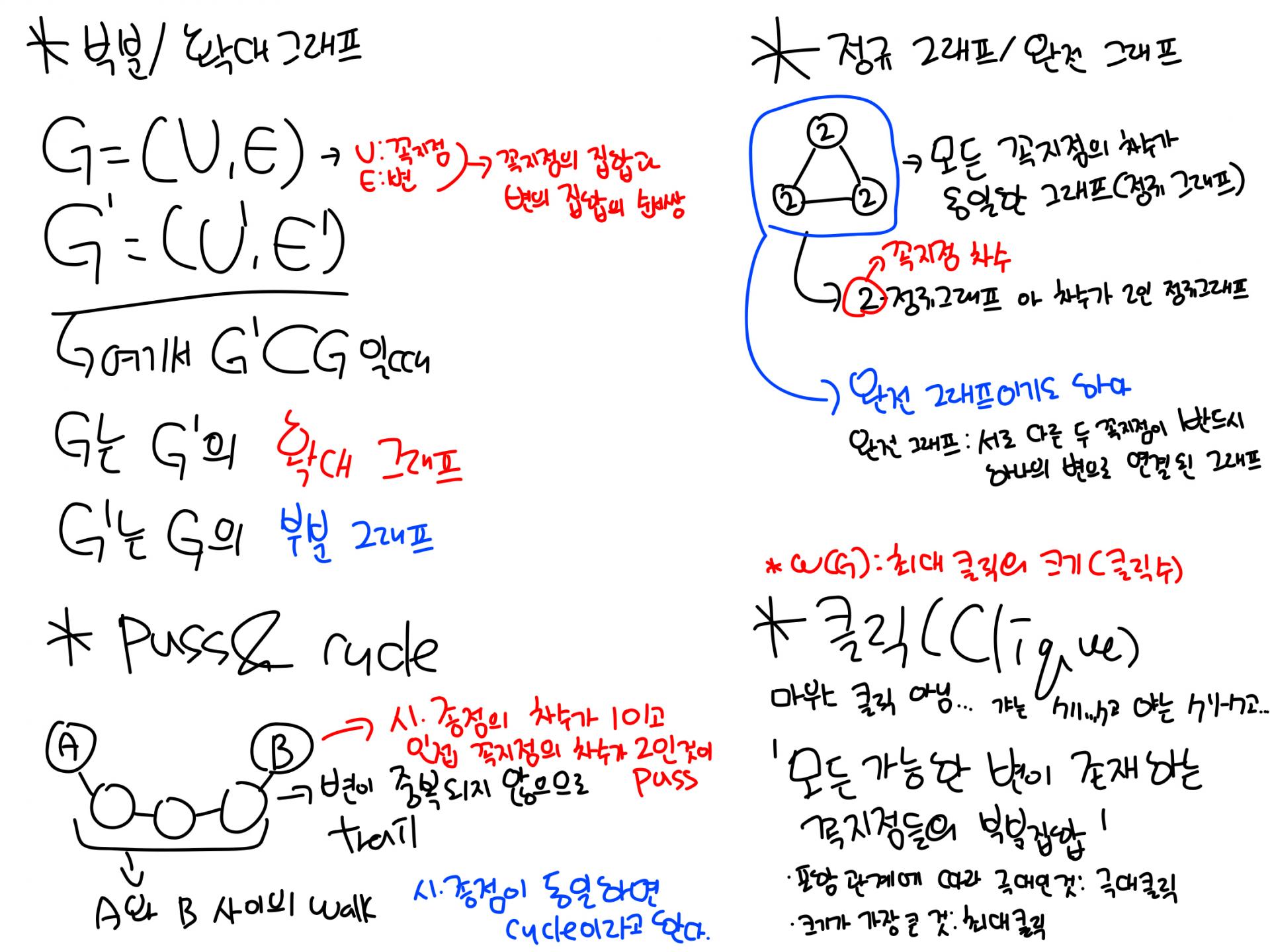
*부분 그래프: 어떤 그래프를 G=(V,E)라고 하고 다른 그래프를 G'=(V',E')라고 할 때, G'가 G의 부분집합인 것. (그러니까 G'의 꼭지점과 변이 G에 포함된 거) 장암-건대입구는 장암-석남의 부분 그래프입니다.
*확대 그래프: (대충 위의 부분 그래프 정의 참고) G는 G'에 대해 확대 그래프이다. 즉 장암-석남은 장암-건대입구의 확대 그래프입니다. 집합으로 치자면 부분집합/부분집합을 포함하는 집합같은 개념...
*정규 그래프: 모든 꼭지점의 차수가 동일한 그래프
*완전 그래프: 서로 다른 두 꼭지점이 하나도 빠짐없이 연결된 그래프(위 예시는 정규 그래프이면서 완전 그래프입니다. 모든 꼭지점의 차수가 같고 전부 연결되어있기 떄문)
*Pass: 시/종점의 차수가 1이고 인접 꼭지점의 차수가 2인 것. 일단 수도권 지하철은 일부 노선을 빼면 pass입니다.
*walk: pass의 시/종점 사이(어린이대공원~장암에서 그 사이에 있는 역들)
*trail: walk간에 중복되는 변이 없는 것(뭔 소리지...)
*cycle: 그래프의 시/종점이 동일한 것(저기 버뮤다 응암지대나 2호선 순환선같은 거)
*클릭: Click 아니고 Clique. '모든 가능한 변이 존재하는 꼭지점들의 부분집합'을 뜻한다는데 저건 또 뭔 소리죠...
*유한/무한 그래프: 꼭지점 개수에 한계가 있으면 유한 그래프, 없으면 무한 그래프(지하철 노선도는 유한 그래프입니다. 어쨌든 꼭지점에 한계가 있으므로...)
*연결 그래프/비연결 그래프: 차수가 0인 꼭지점이 존재하면 비연결 그래프입니다. 일단 지하철 노선도나 버스 노선도는 정류장이 다 연결되어 있으므로 연결 그래프지만, 비연결 그래프일 경우 꼭지점은 있는데 뭔 짓을 해도 거기로 갈 수가 없습니다. 포탈건 쏩시다 거기 애퍼처 사이언스죠
3. 분자 그래프의 예시
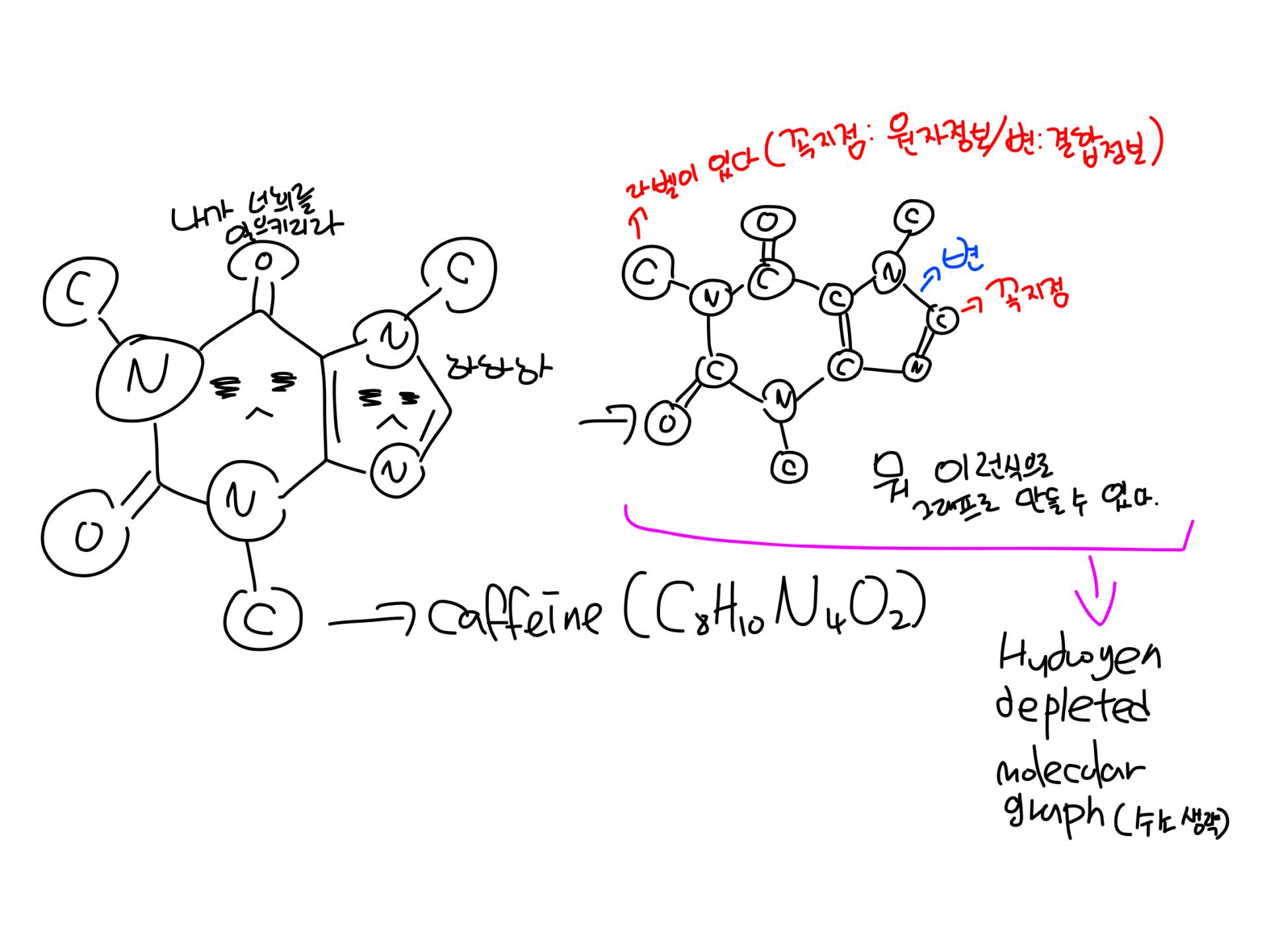
대충 이런 식으로 도식화합니다. 원자가 꼭지점, 결합이 변이고 공유결합이 아니라 charge를 띤 이온이 존재하는 경우에는 변이 없습니다(아래 cTAB처럼). 이중결합은 변을 다중으로 주는 게 아니라, 변은 단일인데 하중을 줘서 표시합니다. 또한 꼭지점의 최외각전자와 변의 하중을 계산해 남는 공간에 '알아서' 수소를 암묵적으로 끼워넣습니다. 그래서 SMILES에서 산소 이온(2가 음이온)이 아니라 O만 달랑 쓰면 물이 됩니다.
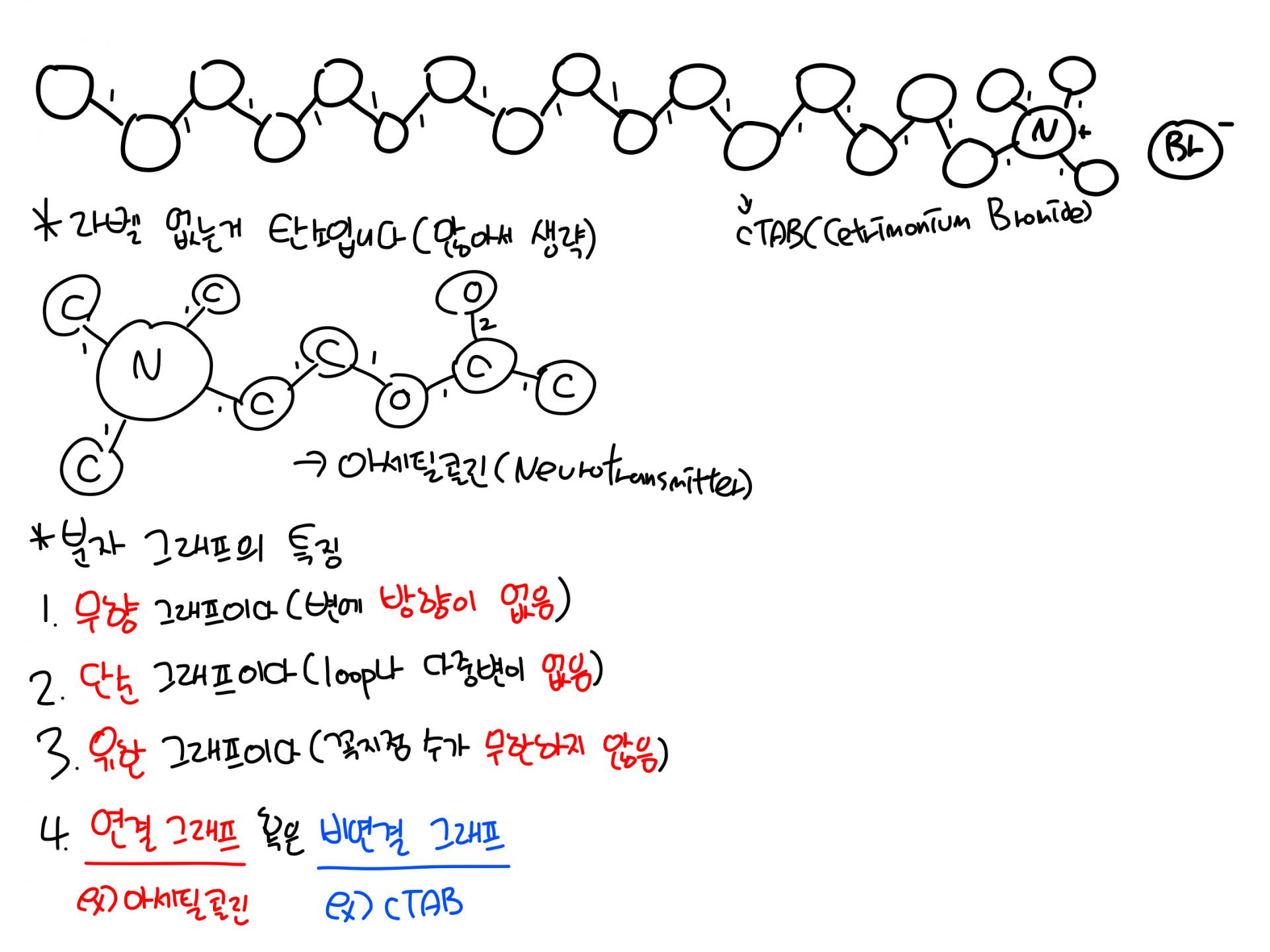
위: cTAB(세트리모늄 브로마이드, 계면활성제인데 DNA 뽑을 때 씁니다)
아래: 아세틸콜린(신경전달물질 중 하나)
아세틸콜린은 연결 그래프이고 cTAB은 비연결 그래프입니다. cTAB의 브로민 꼭지점은 혼자 떨어져 있어서 차수가 0이거든요. 응? 근데 왜 단순이냐고요? 이중결합이면 변 두개 아니냐고요? 아뇨 저기 라벨 붙었는데요? 변을 다중으로 놓은 게 아니라, 결합 수를 하중으로 처리한겁니다. 거기다가 꼭지점에는 원자 라벨이 붙어있어서 이 그래프는 labeled graph입니다. (꼭지점에 이름 있으면 라벨 달린 그래프)
4. 분자 그래프의 구축 방식
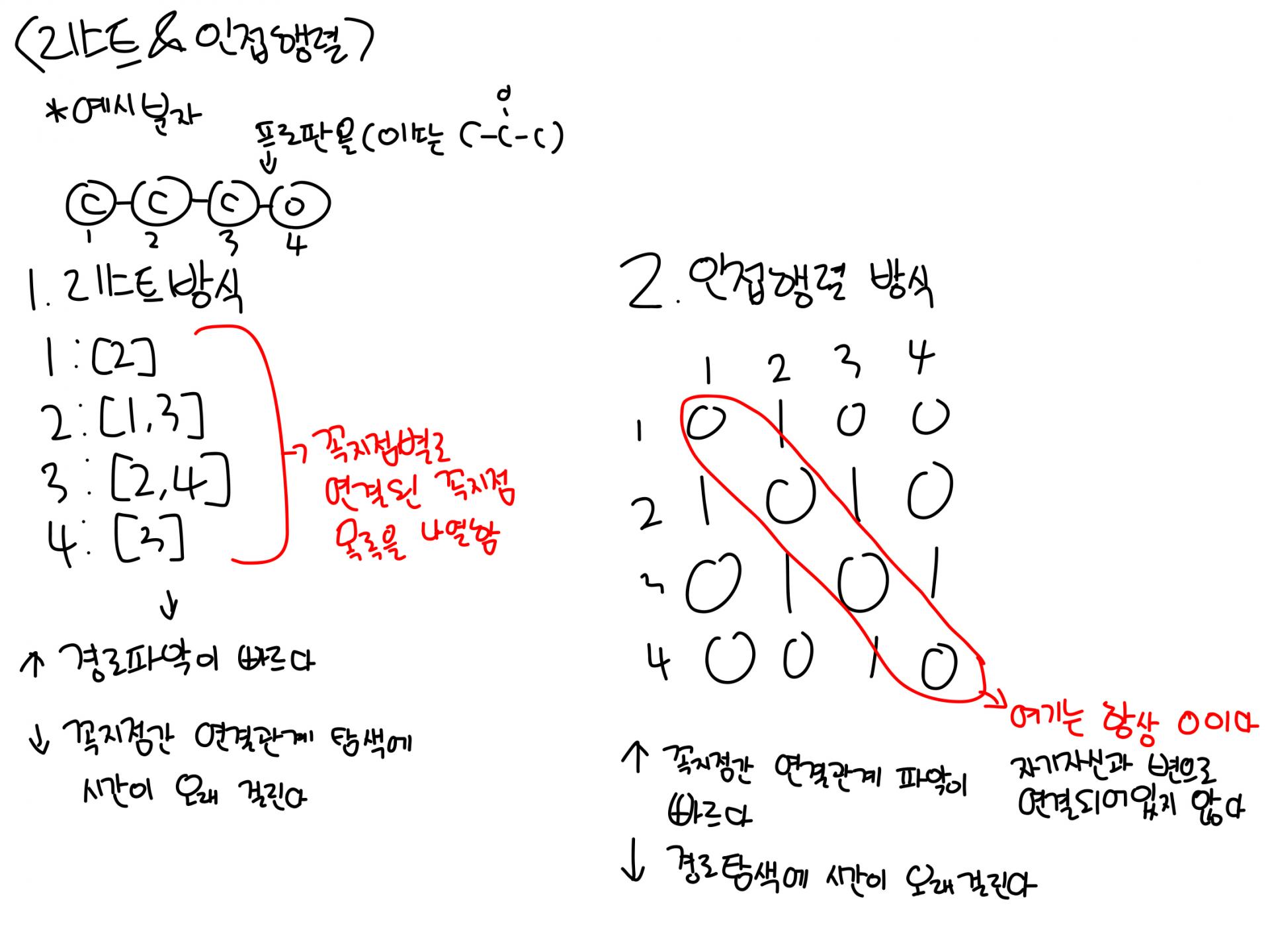
SMILES는 텍스트이기때문에 이걸 그림으로 만들려면 한번 재구축 과정을 거쳐야 합니다. 컴퓨터가 인간의 말을 못 알아듣고, 인간은 기계어나 어셈블리어를 못 하기때문에 중간에서 프로그래밍 언어 통해서 얘기하는 거랑 비슷합니다. 물론 기계어나 어셈블리어는 할 수 있는 굇수들이나 있지...
구축 방식은 리스트와 인접 행렬로 나뉘는데, 리스트는 꼭지점별로 연결된 꼭지점을 목록 형태로 나열하는 방식이고 인접 행렬은 꼭지점과 다른 꼭지점의 연결 관계를 행렬로 나타내는 방식입니다. 0이면 연결이 없는거고, 1이면 연결이 있는거죠. 위 예시의 1번 탄소는 2번 탄소와 연결되어 있으므로 1행 2열만 1입니다. 참고로 인접행럴의 주대각선은 자기 자신과 루프로 연결되어 있지 않은 이상 0이고, 분자 그래프는 루프가 없습니다.
리스트 방식은 경로 탐색이 빨리 되지만 연결 관계를 파악하는 데 오래 걸리고, 인접행렬 방식은 리스트와 반대로 연결 관계를 빨리 파악할 수 있지만 연결 관계를 파악하는 데 오래 걸립니다. 보통 딥러닝 관련 논문에서는 인접행렬을 많이 쓰고 리스트는... 내가 저거 PDB 파일에서 하나 본 거 같은데?







그래프 이론 용어들이 뭔 말인지는 모르겠는데, 저 노선도 달월역 미개통인 거 보면 오래돼도 8년 가까이 된 엄청 오래된 물건인데요...?