- 0
- 국내산라이츄
- 조회 수 870

실로 간만의 연재군요.
타이틀 새로 그려야되는데 요즘 평일에는 다음날 일해야해서 그림을 못 그리고, 주말에는 귀찮아서 안 그립니다.
1. GCD, LCM
영문 약자라서 이게 뭔 dog sound인가 싶으실텐데, 이거 최대공약수(GCD)랑 최소공배수(LCM)입니다. 초닥교때 다 배웠다 그죠? 근데 솔직히 까먹었다 그죠옹?
약수는 어떤 수를 나머지 없이 나누는 수를 말합니다. 6의 약수는 1, 2, 3, 6이죠.
공약수는 두 수의 공통된 약수를 말합니다. 6과 9의 공약수는 1, 3이죠. 그리고 최대공약수는 공약수 중에서 제일 큰 수입니다.
배수는 어떤 수를 자연수로 곱하면 그게 배수입니다. 5, 10, 15, 20, 25,...는 전부 5의 배수죠.
공배수는 두 수의 공통된 배수를 말합니다. 6과 9의 공배수는 18, 36, 54, ...입니다. 그리고 최소공배수는 공배수 중에서 제일 작은 공배수를 가리킵니다.
반대되는 개념이 왜 없냐면 최소공약수는 1이고 최대공배수는 수가 끝이 없어서 없습니다.
2. 유클리드 호제법?
유클리드 호제법은 두 수를 서로(互) 나눠서(除) 최대공약수를 구하는 방법입니다. 기술된 알고리즘 중에서는 가장 오래된 알고리즘으로 알려져 있죠. 대충 호랑이 담배 배우던 시절에 나온겁니다.
보통 최대공약수 구할 때 어떻게 하시나요?
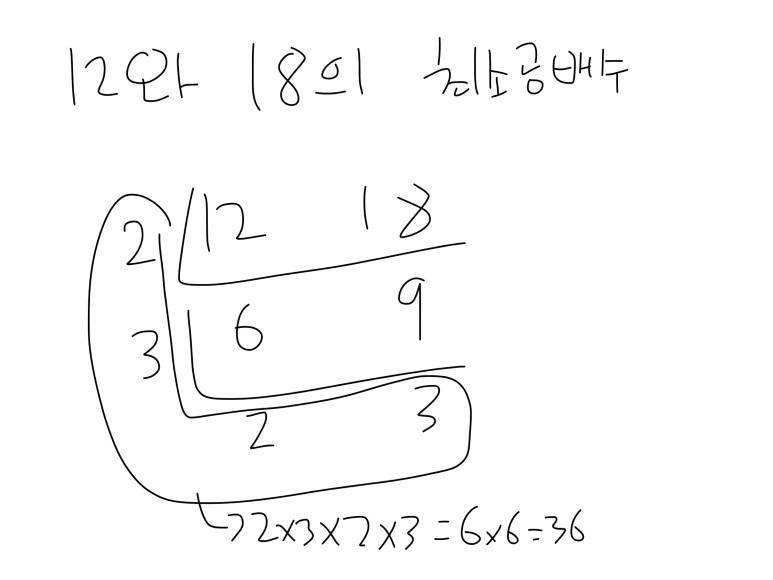
그죠 초닥교때는 이렇게 했죠. 그리고 머리 좀 굵어지면 소인수분해로 구했다 그죠? 근데 생각해봅시다. 18과 30의 최대공약수는 얼마인가요? 하면 척수반사로 6! 하는데... 누가요 제가요 뜬금없이 210과 297의 최대공약수 이런거 물어보면 어떻게 하나요?

질문자를 이러고 봅니다. 근데 우리가 유클리드 호제법을 알고 있다면 질문자를 이렇게 볼 필요가 없습니다.
3. 어떻게 구하나요?

위에서 두 수를 서로 나눠서 최대공약수를 구하는 방법이라고 했는데, 말 그대로입니다. 위 과정이 유클리드 호제법을 이용해서 210와 297의 최대공약수를 구하고 그걸 바탕으로 최소공배수를 계산하는 과정인데, 1번을 보면 297 = 210+87이죠? 그러면 이제 210을 87로 나누게 됩니다. 그래서 두번째 줄에서는 210을 87*2와 36으로 나타냈고, 세번째 줄에서는 87을 36과 15로, 그 다음 줄에서는 36을 15와 6으로, 또 그 다음 줄에서는 15를 6과 3으로, 그리고 마지막 줄에서는 6이 3의 배수이기 때문에 드디어 끝났습니다. 예. 그래서 210와 297의 최대공약수는 3이 되었습니다. 최소공배수는 최대공약수 구했으니까 나눠서 곱하면 됩니다.
사실 297이 3의 배수이기때문에 일단 3은 끼고 들어가는 게 맞긴 합니다. 2+9+7=18이잖아요.

만약 어떤 수가 서로소라면 마지막 줄에서 0으로 나누어 떨어지지 않게 됩니다. 그래서 n * 1의 형태가 되는데 이렇게 나오면 두 수는 서로소인겁니다. 즉, 1025와 99는 서로소가 되겠습니다. (서로소: 두 수의 공약수가 1밖에 없는 수)
 포함 1명이 추천
포함 1명이 추천




